Hình bình hành là gì? Dấu hiệu nhận thấy hình bình hành? Tính hóa học của hình bình hành? Cách tính diện tích S hình bình hành? Cách tính chu vi hình bình hành? Khi với những vướng mắc này, Quý fan hâm mộ chớ bỏ dở những share của Cửa Hàng chúng tôi nhập bài xích viết:
Hình bình hành là gì?
Hình bình hành (hay thường hay gọi là hình tứ giác đều) là một trong những hình học tập phẳng lặng với tư cạnh tuy vậy song và đều bằng nhau, và những góc mặt mày đối lập đều bằng nhau. Hình bình hành với hai tuyến đường chéo cánh tách nhau ở trung điểm của từng lối chéo cánh và phân tách tạo hình tư tam giác đồng dạng.
Bạn đang xem: dấu hiệu nhận biết hình bình hành
Công thức tính diện tích S hình bình hành là S = hạ tầng x lối cao, nhập bại liệt hạ tầng là phỏng nhiều năm của một cạnh, lối cao là khoảng cách từ là một đỉnh cho tới cạnh đối lập. Hình bình hành được dùng thoáng rộng nhập toán học tập và trong những phần mềm nghệ thuật.
Tính hóa học của hình bình hành
Dưới đấy là một vài đặc thù của hình bình hành:
– Các cạnh đối lập của hình bình hành là tuy vậy song và đều bằng nhau.
– Các góc đối lập của hình bình hành là đều bằng nhau.
– Hai lối chéo cánh của hình bình hành với nằm trong phỏng nhiều năm và tách nhau bên trên trung điểm của từng lối chéo cánh.
– Hình bình hành với nhì trục đối xứng, này là lối chéo cánh rộng lớn và lối chéo cánh nhỏ.
– Diện tích của hình bình hành vì chưng tích của phỏng nhiều năm cạnh và phỏng nhiều năm lối cao ứng với cạnh bại liệt.
– Chu vi của hình bình hành vì chưng tổng phỏng nhiều năm tư cạnh của chính nó.
– Hình bình hành là một trong những dạng nhiều diện lồi (convex polygon).
– Hình bình hành rất có thể được đổi khác trở nên một hình vuông vắn Khi lối chéo cánh của chính nó là 2 lần bán kính của hình vuông vắn bại liệt.
Các đặc thù này được dùng thoáng rộng trong những việc giải quyết và xử lý những Việc tương quan cho tới hình bình hành.
Cách minh chứng hình bình hành
Để minh chứng một hình thang minh chứng này bại liệt là một trong những hình bình hành, tất cả chúng ta cần thiết minh chứng rằng nó thỏa mãn nhu cầu những đặc thù sau:
– Các cạnh đối lập đều bằng nhau và tuy vậy song cùng nhau.
– Các góc đối lập đều bằng nhau.
– Hai lối chéo cánh tách nhau bên trên trung điểm của từng lối chéo cánh.
– Các lối chéo cánh có tính nhiều năm đều bằng nhau.
Để minh chứng đặc thù loại nhất và loại nhì, tớ rất có thể dùng những lăm le lí hình học tập hoặc vì chưng cách thức đối ngẫu.
Để minh chứng đặc thù loại thân phụ, tớ rất có thể dùng lăm le lí về lối trung trực. Với một hình thang ABCD, tớ vẽ lối chéo cánh AC và BD. Vì ABCD là một trong những hình thang, nên lối trung trực của AB tách lối trung trực của CD bên trên một điểm E, và lối trung trực của BC tách lối trung trực của AD bên trên một điểm F. Vì AE = EC và BF = FD, nên điểm G là trung điểm của CE và điểm H là trung điểm của DF. Do bại liệt, AG và DH là hai tuyến đường chéo cánh của hình thang ABCD và bọn chúng tách nhau bên trên trung điểm I của từng lối chéo cánh.
Để minh chứng đặc thù loại tư, tớ cũng rất có thể dùng những lăm le lí hình học tập. Ví dụ, tớ rất có thể dùng lăm le lí về tam giác đều, vì như thế Khi phân tách hình thang ABCD trở nên nhì tam giác đều bằng nhau vì chưng lối chéo cánh AC, tớ chiếm được nhì tam giác đều AEC và BFD. Do bại liệt, tớ với CE = DF, và AG và DH là lối trung trực của CE và DF ứng, nên AG = DH. Vì vậy, hai tuyến đường chéo cánh của hình thang ABCD có tính nhiều năm đều bằng nhau.
Như vậy, nếu như một hình thang vừa lòng những đặc thù bên trên, thì nó là một trong những hình bình hành.
Dấu hiệu nhận thấy hình bình hành
1/ Tứ giác với những cạnh đối tuy vậy song là hình bình hành.
Tứ giác ABCD với AB//CD và AD//CB thì ABCD là hình bình hành.
2/ Tứ giác với những cạnh đối đều bằng nhau là hình bình hành.
Tứ giác ABCD với AB = CD, AD =BC thì ABCD là hình bình hành.
3/ Tứ giác với nhì cạnh đối tuy vậy song và đều bằng nhau là hình bình hành.
Tứ giác ABCD với AB//CD và AB = CD hoặc AD//BC và AD = BC thì ABCD là hình bình hành.
4/ Tứ giác với những góc đối đều bằng nhau là hình bình hành.
Tứ giác ABCD có thì ABCD là hình bình hành.
5/ Tứ giác với hai tuyến đường chéo cánh tách nhau bên trên trung điểm của từng lối là hình bình hành.
Tứ giác ABCD với AC tách BD bên trên O. Nếu OA = OC, OB = OD thì ABCD là hình bình hành.
Hình bình hành với trục đối xứng không?
Có, hình bình hành với nhì trục đối xứng. Hai trục này là lối chéo cánh rộng lớn và lối chéo cánh nhỏ. Khi cù hình bình hành xoay xung quanh lối chéo cánh rộng lớn, những đối xứng của chính nó tiếp tục trùng cùng nhau Khi cù một góc là 180 phỏng. Tương tự động, Khi cù hình bình hành xoay xung quanh lối chéo cánh nhỏ, những đối xứng của chính nó cũng tiếp tục trùng cùng nhau Khi cù một góc là 180 phỏng. Do bại liệt, hình bình hành rất có thể được xem như là một hình đối xứng.
Tính hóa học lối chéo cánh hình bình hành
Đường chéo cánh của hình bình hành là đoạn trực tiếp nối nhì đỉnh ko kề nhau của hình. Hình bình hành với hai tuyến đường chéo cánh đó là lối chéo cánh rộng lớn và lối chéo cánh nhỏ. Dưới đấy là một vài đặc thù của lối chéo cánh nhập hình bình hành:
– Hai lối chéo cánh của hình bình hành có tính nhiều năm đều bằng nhau.
– Đường chéo cánh phân tách hình bình hành trở nên nhì tam giác đều và đồng dạng cùng nhau.
– Độ nhiều năm lối chéo cánh rộng lớn vì chưng tích căn bậc nhì của tổng bình phương phỏng nhiều năm nhì cạnh kề của hình bình hành.
– Độ nhiều năm lối chéo cánh nhỏ vì chưng tích căn bậc nhì của tổng bình phương phỏng nhiều năm hai tuyến đường cao ứng với nhì cạnh kề của hình bình hành.
Các đặc thù này vô cùng hữu ích trong những việc giải những Việc tương quan cho tới hình bình hành và lối chéo cánh của chính nó.
Diện tích hình bình hành
Diện tích hình bình hành được đo vì chưng kích cỡ của mặt phẳng hình, là phần mặt mày phẳng lặng tớ rất có thể bắt gặp của hình bình hành.
Diện tích hình bình hành được xem theo đuổi công thức bằng tích của cạnh lòng nhân với độ cao.
SABCD = a.h
Xem thêm: u cà na
Trong đó:
+ S là diện tích S hình bình hành
+ a là cạnh lòng của hình bình hành
+ h là độ cao nối tử đỉnh cho tới lòng của một hình bình hành.
Chu vi hình bình hành
Chu vi hình bình hành được tính vì chưng tổng phỏng nhiều năm những lối xung quanh hình, cũng đó là lối xung quanh toàn cỗ diện tích S, vì chưng gấp đôi tổng một cặp cạnh kề nhau ngẫu nhiên. Nói cách tiếp theo, chu vi hình bình hành là tổng phỏng nhiều năm của 4 cạnh.
Công thức rõ ràng như sau:
C = 2 x (a+b)
Trong đó:
+ C là chu vi hình bình hành.
+ a và b là cặp cạnh kề nhau của hình bình hành.
Bài tập dượt về hình bình hành
Bài tập dượt 1: Trong những tứ giác sau, tứ giác này là hình bình hành? Vì sao?
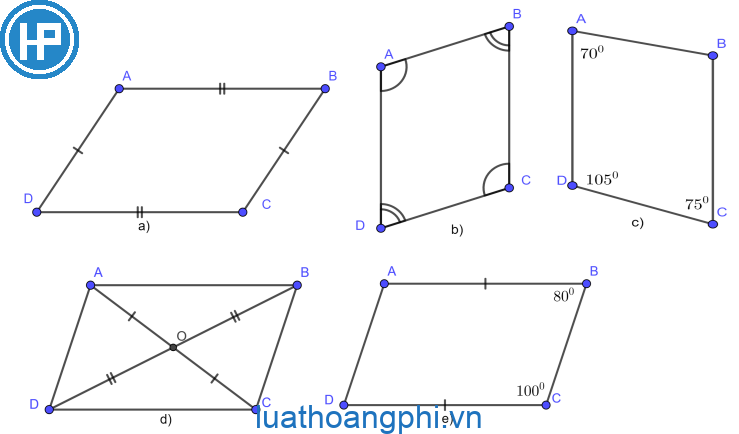
Hướng dẫn:
a) Tứ giác ABCD với AB = CD, BC = AD bởi vậy ABCD là hình bình hành.
b) Tứ giác ABCD có do bại liệt ABCD là hình bình hành.
c) Tứ giác ABCD có nên AB và CD ko tuy vậy tuy vậy. Suy rời khỏi, ABCD ko cần hình bình hành
d) Tứ giác ABCD với hai tuyến đường chéo cánh là AC vad BD. AC phó BD bên trên O. Ta có: OA = OC, OB = OD nên ABCD là hình bình hành.
e) Tứ giác ABCD có nên AB tuy vậy song với CD, tuy nhiên AB = CD suy rời khỏi ABCD là hình bình hành.
Bài tập dượt 2: Tứ giác ABCD với E, F, G, H theo đuổi trật tự là trung điểm của những cạnh AB, BC, CD, DA. Tứ giác EFGH là hình gì? Vì sao?
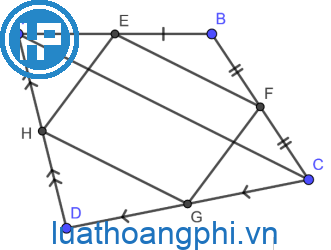
Hướng dẫn:
Xét tam giác ABC có:
E là trung điểm AB
F là trung điểm BC
Suy rời khỏi, EF là lối tầm của tam giác ABC
=> EF // AC, EF = ½ AC (1)
Xét tam giác ACD có:
H là trung điểm của AD
G là trung điểm củ CD
Suy rời khỏi, HG là lối tầm của tam giác ACD
HG // CD, HG = ½ CD (2)
Từ (1) và (2) suy rời khỏi, EF//HG và EF = HG
Xét tứ giác EFGH có: EF//HG và EF = HG
Suy rời khỏi, EFGH là hình bình hành.
Bài tập dượt 3:
Cho hình bình hành với cạnh lòng vì chưng 12cm, cạnh mặt mày vì chưng 7cm, độ cao vì chưng 5cm. Hãy tính chu vi và diện tích S của hình bình hành đó?
Hướng dẫn:
Chu vi của hình bình hành là:
Xem thêm: cách nấu gạo lứt
P = 2( 12 + 7) = 38 (cm)
Diện tích hình bình hành là:
S = a.h = 12.5 = 60 (cm2)













Bình luận