công thức nhị thức newton

By Admin 17/08/2023 0

Bài viết lách tiếp sau đây reviews cho tới chúng ta công thức khai triển nhị thức Newton và một trong những dạng toán thông thường gặp gỡ. Các các bạn bám theo dõi nội dung bài viết nhằm thám thính hiểu thêm thắt nhé!

I. CÔNG THỨC NHỊ THỨC NEWTON

Với n là số nguyên vẹn dương. Hai số a, b là những số thực. Ta với công thức:

Bạn đang xem: công thức nhị thức newton

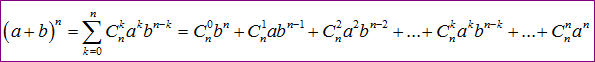
công thức nhị thức newton lớp 11

Vì tầm quan trọng của a và b như nhau nên hoán thay vị trí a và b tớ với công thức tương tự.

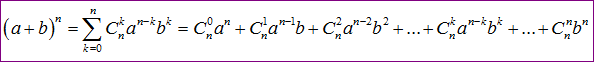
các công thức nhị thức newton

Để dễ dàng lưu giữ thì chúng ta nhằm ý trong những số hạng tổng số nón của a và b luôn luôn vì chưng n. Và trong những khai triển với n+1 số hạng.

Áp dụng công thứckhai triển nhị thức newton bên trên tớ rất có thể đơn giản và dễ dàng khai triển 1 số ít hằng đẳng thức quen thuộc thuộc:

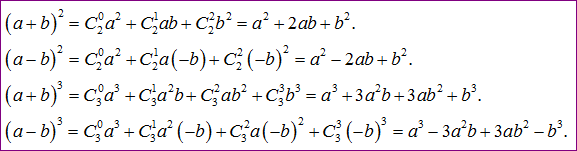
nhị thức newton cơ bản

II. CÁC BÀI TOÁN VỀ NHỊ THỨC NEWTON

Dạng 1. Tìm thông số nhập khai triển-Tìm số hạng nhập khai triển

Với dạng toán này, chúng ta hãy dùng số hạng tổng quát lác (số hạng loại k+1) của khai triển. Sau cơ thay đổi nhằm tách riêng biệt phần thay đổi và phần thông số. Cuối nằm trong nhờ vào đề bài xích nhằm xác lập chỉ số k. Lưu ý số hạng bao gồm hệ số+phần thay đổi.

Ví dụ 1:

Tìm số hạng ko chứa chấp x nhập khai triển của nhị thức

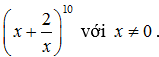
công thức nhị thức niu tơn

Lời giải:

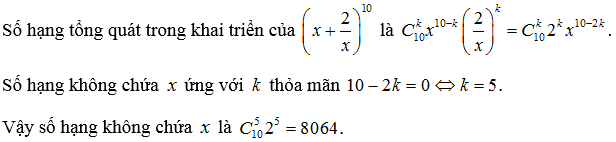
nhị thức newton thám thính hệ số

Ví dụ 2:

Xem thêm: u cà na

Tìm số hạng chứa chấp x³ nhập khai triển của nhị thức

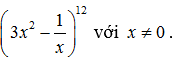
Lời giải:

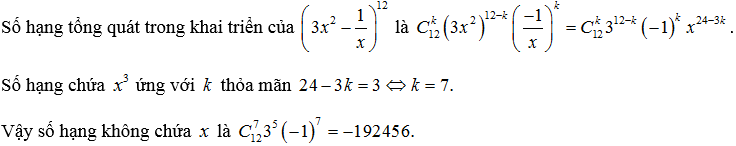
Dạng 2. Một số vấn đề tương quan cho tới khai triển lũy quá của (1+x)

Đây là 1 trong khai triển hoặc được dùng nhằm giải 1 số ít vấn đề tương quan cho tới nhị thức Νewton.

Ví dụ:

Với n là số nguyên vẹn dương, chứng tỏ rằng:

cách khai triển nhị thức newton

Lời giải:

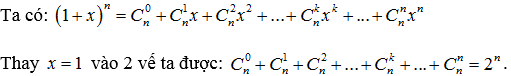
Trên đấy là công thức khai triển nhị thức Νewton và một trong những vấn đề tương quan. Kiến thức thì vô hạn. Một nội dung bài viết cụt với xíu này chắc hẳn rằng ko thể hiện tại không còn được kiến thức và kỹ năng về nhị thức Νewton. Nhưng này là những kiến thức và kỹ năng cơ phiên bản nhất nhưng mà chúng ta cần nắm được. Chúc chúng ta học tập chất lượng và trở nên công!

Xem thêm:

Xem thêm: uống nước tía to bao nhiều là đủ

Quy tắc đếm: Quy tắc nằm trong và quy tắc nhân

Bài luyện nhị thức Niu tơn (Newton) thám thính số hạng

Tính tổng tương quan cho tới nhị thức Newton (Niu tơn)