Đường trung tuyến của tam giác là một trong những trong mỗi con kiến thức cơ phiên bản tuy nhiên học viên nên nắm rõ nhằm áp dụng vô những bài bác luyện, bài bác đua. Nếu chúng ta quên, chớ phiền lòng vì thế nội dung bài viết này tiếp tục giúp cho bạn gia tăng con kiến thức cộng đồng của tớ về đàng trung tuyến là gì? Các đặc điểm về đàng trung tuyến vô tam giác là gì? Các dạng bài bác luyện về đàng trung tuyến vô tam giác nhất là gì?
Đường trung tuyến của đoạn thẳng là một đường thẳng liền mạch trải qua trung điểm của đoạn trực tiếp bại.
Bạn đang xem: đường trung tuyến trong tam giác cân
Định nghĩa đàng trung tuyến của tam giác?
Đường trung tuyến vô tam giác là một quãng trực tiếp nối kể từ đỉnh của tam giác cho tới của cạnh đối lập. Mỗi tam giác sẽ sở hữu được 3 đàng trung tuyến.
Tính hóa học của đàng trung tuyến vô tam giác
Đường trung tuyến của một tam giác gồm có 3 tính chất đó là:
- Ba đàng trung tuyến của tam giác nằm trong trải qua một điểm. Điểm bại cơ hội đỉnh một khoảng chừng vị phỏng nhiều năm đàng trung tuyến trải qua đỉnh ấy.
- Giao điểm của tía đàng trung tuyến gọi là trọng tâm.
- Vị trí trọng tâm của tam giác: Trọng tâm của một tam giác cơ hội từng đỉnh một khoảng chừng vị phỏng nhiều năm đàng trung tuyến trải qua đỉnh ấy.
VD:
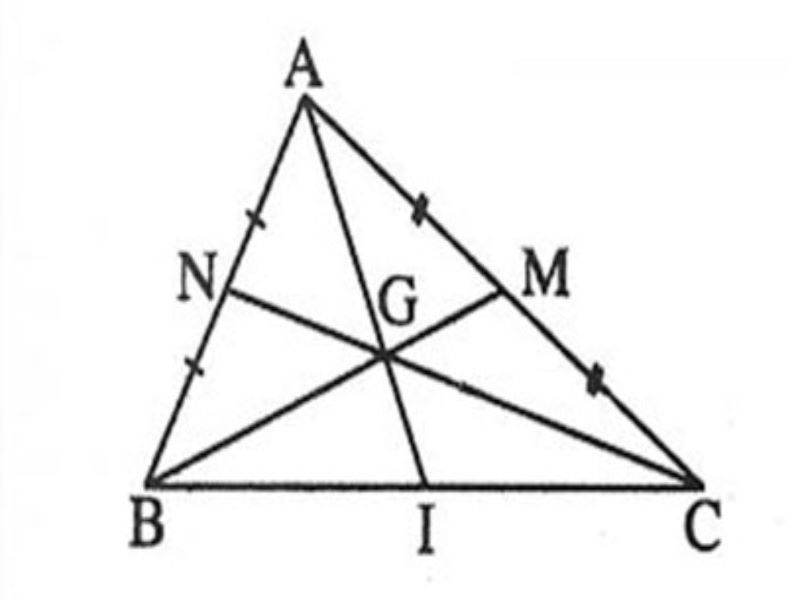
Vì G là trọng tâm của tam giác ABC, ABC và với những trung tuyến AI, BM, công nhân nên tao sẽ sở hữu được biểu thức: AG/AI = BG/BM = CG/CN = 2/3
Một số toan lý đàng trung tuyến vô tam giác
Trong tam giác, đường trung tuyến có 3 định lý đó là:
- Ba đàng trung tuyến của một tam giác nằm trong trải qua một điểm. gọi là trọng tâm của tam giác bại.
- Đường trung tuyến của tam giác phân chia tam giác ấy trở thành nhị tam giác với diện tích S đều nhau. Ba trung tuyến phân chia tam giác trở thành 6 tam giác nhỏ với diện tích S đều nhau.
- Về địa điểm trọng tâm: Trọng tâm của một tam giác cơ hội từng đỉnh một khoảng chừng vị phỏng nhiều năm đàng trung tuyến qua chuyện đỉnh ấy.
Định nghĩa đàng trung tuyến vô tam giác quánh biệt
Tìm hiểu đàng trung tuyến vô tam giác vuông
Tính hóa học đàng trung tuyến vô tham ô giác vuông:
- Trong tam giác vuông, trung tuyến ứng với cạnh huyền vị một nửa cạnh huyền.
- Một tam giác với trung tuyến ứng với cùng 1 cạnh vị nửa cạnh bại thì tam giác ấy là tam giác vuông.
- Đường trung tuyến của tam giác vuông với tương đối đầy đủ những đặc điểm của một đàng trung tuyến tam giác.
VD: 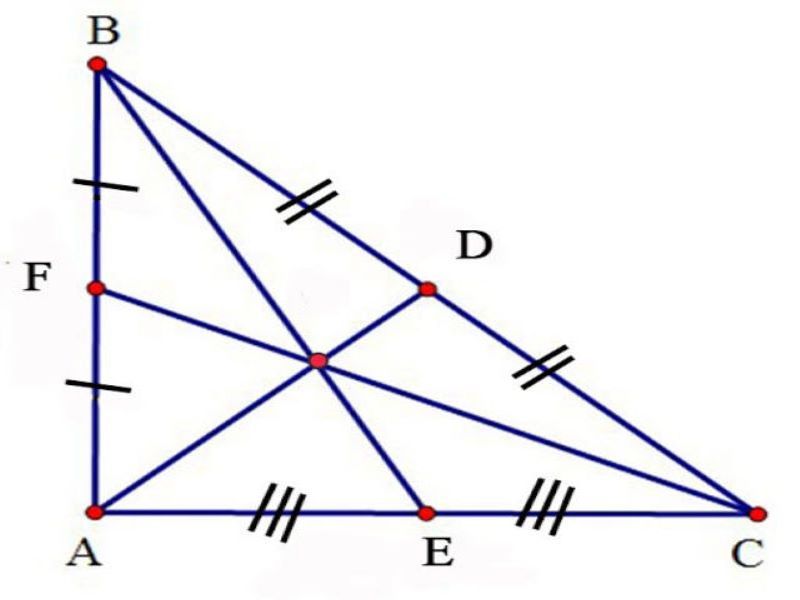
ABC vuông với AD là trung tuyến ứng với cạnh huyền BC.
=> AD = 1/2BC = DB = DC
Ngược lại, nếu như trung tuyến AM = 1/2BC thì ABC vuông bên trên A.
Tìm hiểu đường trung tuyến trong tam giác cân, tam giác đều
Tính hóa học đường trung tuyến trong tam giác cân:
Đường trung tuyến ứng với cạnh lòng thì vuông góc với cạnh lòng. Và phân chia tam giác trở thành 2 tam giác đều nhau.
VD: 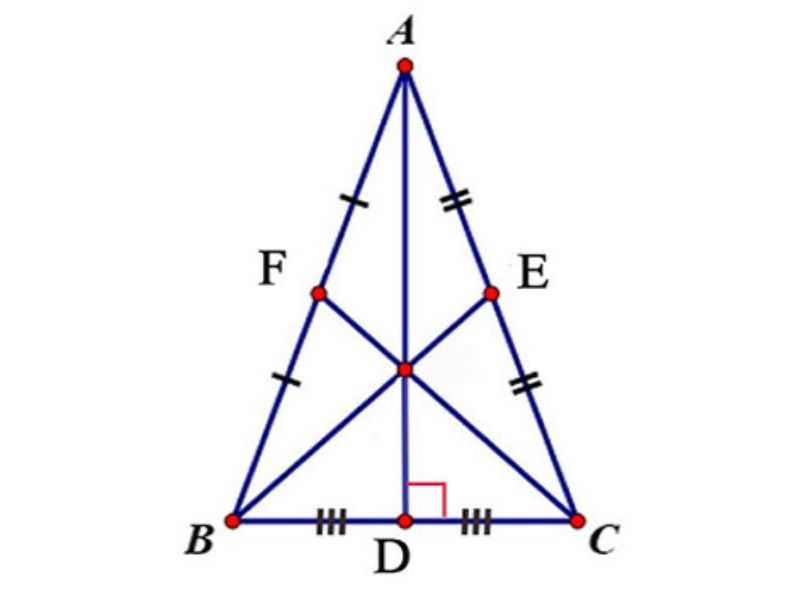
ABC cân nặng bên trên A với đàng trung tuyến AD ứng với cạnh BC=> AD ⊥ BC và ΔADB = ΔADC
Tính hóa học đàng trung tuyến vô tam giác đều:
- 3 đàng trung tuyến của tam giác đều tiếp tục phân chia tam giác bại trở thành 6 tam giác với diện tích S đều nhau.
- Trong tam giác đều đường thẳng liền mạch trải qua một đỉnh ngẫu nhiên và trải qua trọng tâm của tam giác tiếp tục phân chia tam giác bại trở thành 2 tam giác với diện tích S đều nhau.
VD: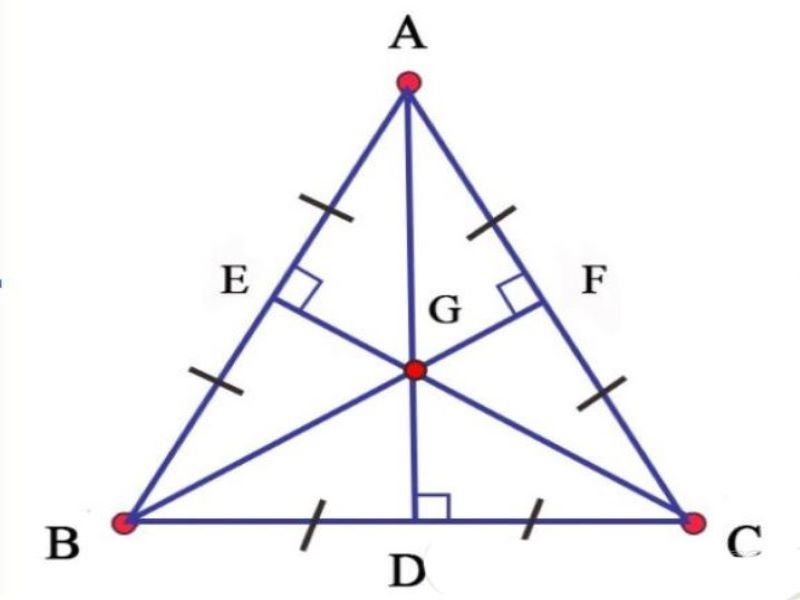
ΔABC đều => ΔGAE = ΔGAF = ΔGCF = ΔGCD = ΔGBD = ΔGBE = ΔGEB = ΔGEA
SADB = SADC = SCEA = SCEB = SBFA = SBFC
Công thức tương quan cho tới phỏng nhiều năm của trung tuyến
Chúng tao rất có thể tính được phỏng nhiều năm đàng trung tuyến của cạnh ngẫu nhiên bằng phương pháp lấy căn bậc 2 của một trong những phần nhị tổng bình phương nhị cạnh kề trừ một trong những phần tư bình phương cạnh đối (Định lý Apollonnius)
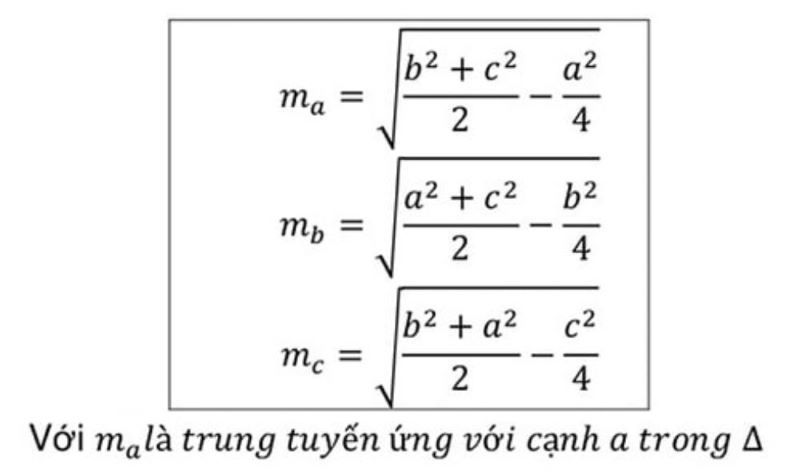
Trong đó: a, b ,c theo thứ tự là những cạnh vô tam giác
ma, mb, mc lần lượt là những đàng trung tuyến vô tam giác
Các dạng toán thông thường gặp gỡ về đàng trung tuyến
Dạng 1: Tìm những tỉ trọng trong số những cạnh và tính phỏng nhiều năm của đoạn thẳng
Phương pháp giải: Chú ý cho tới địa điểm trọng tâm của tam giác, xác lập 3 đàng trung tuyến của tam giác
Xem thêm: uống nước tía to bao nhiều là đủ
VD: Cho G là trọng tâm của tam giác đều ABC. Chứng minh rằng GA = GB = GC?
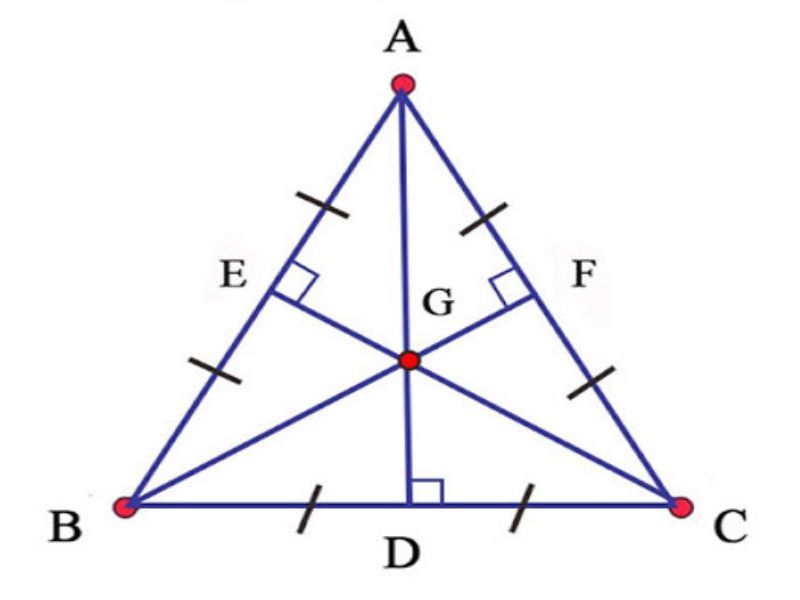
Bài giải:
Gọi AD, CE, BF là những đàng trung tuyến tam giác ABC hoặc D, E, F theo thứ tự là trung điểm cạnh BC, AB, AC
+Ta với AD là đàng trung tuyến tam giác ABC nên AG= 2/3AD (1)
+CE là đàng trung tuyến tam giác ABC nên CG= 2/3CE(2)
+BF là đàng trung tuyến tam giác ABC nên BG= 2/3BF(3)
Ta với ΔBAC đều =>AD = BF = CE (4)
Từ (1), (2), (3), (4) suy rời khỏi AG = BG = CG
Dạng 2: Đường trung tuyến với những tam giác quánh biệt
Phương pháp giải:
- Trong tam giác vuông: Xác toan đàng trung tuyến ứng với cạnh huyền.
- Trong tam giác cân nặng, tam giác đều: Xác toan được trung tuyến ứng với cạnh lòng và phân chia tam giác trở thành nhị tam giác đều nhau.
VD: Cho tam giác ABC cân nặng ở A có AB = AC = 17cm, BC= 16cm. Kẻ trung tuyến AM?
a) Chứng minh: AM ⊥ BC?
b) Tính độ dài AM?
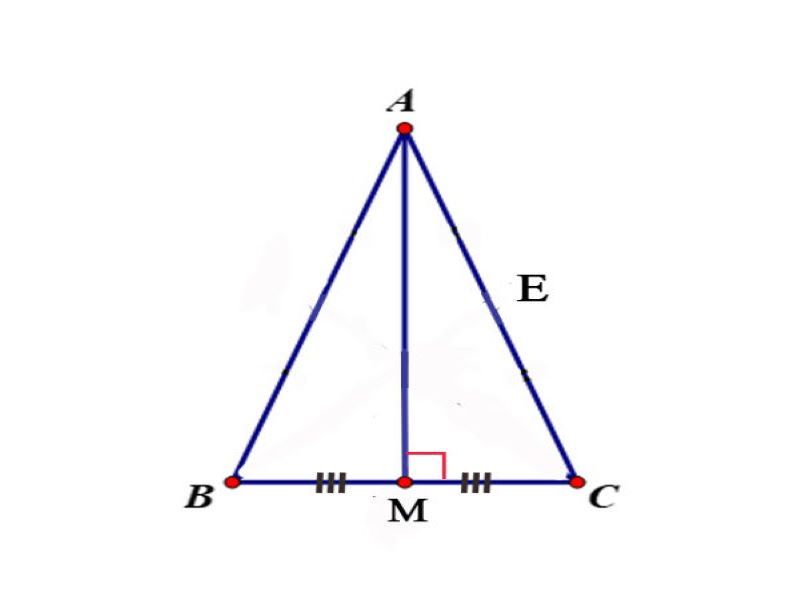
Bài giải:
a) Ta với AM là đàng trung tuyến ABC nên MB = MC
Mặt không giống ABC cân nặng bên trên A
=> AM vừa vặn là đàng trung tuyến vừa vặn là đàng cao
Vậy AM ⊥ BC
b) Ta có:
+BC = 16cm nên BM = MC = 8cm
+AB = AC = 17cm
Xét tam giác AMC vuông bên trên M
Áp dụng Định lý Pitago có:
Xem thêm: tác dụng của bột sắn dây
AC2 = AM2 + MC2 => 172= AM2 + 82 => AM2 = 172- 82= 225 =>AM= 15Cm.
Xem thêm:
- Đề đánh giá học tập kì 1 môn toán lớp 3 lịch trình mới nhất 2022-2023 với đáp án
- 7 cơ hội viết lách ký hiệu toán học tập vô word giản dị thời gian nhanh chóng
- 10 cơ hội học tập đảm bảo chất lượng toán hiệu suất cao nhất cho tất cả những người thất lạc gốc
Thông qua chuyện nội dung bài viết thời điểm ngày hôm nay, tất cả chúng ta rất có thể lưu giữ lại và xem xét lại những lý thuyết về đàng trung tuyến. Hy vọng những con kiến thức có lợi này sẽ hỗ trợ chúng ta ôn luyện và tập luyện con kiến thức một cơ hội rất tốt, hiệu suất cao nhất nhằm đạt được không ít kết quả mang đến phiên bản thân mật bản thân nhé!












Bình luận